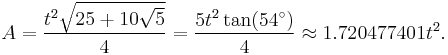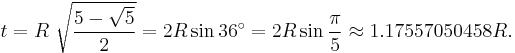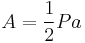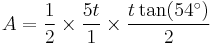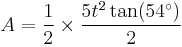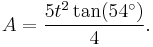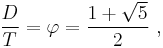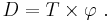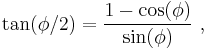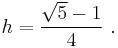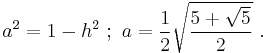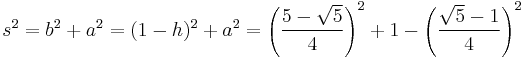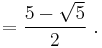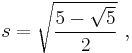Pentagon

Regular pentagon
Regular pentagon.svg
A regular pentagon
Edges and vertices 5
Schläfli symbol {5}
Coxeter–Dynkin diagram CDW ring.pngCDW 5.pngCDW dot.png
Symmetry group Dihedral (D5)
Internal angle
(degrees)		 108°
Properties convex, cyclic, equilateral, isogonal, isotoxal

In geometry, a pentagon is any five-sided polygon. A pentagon may be simple or self-intersecting. The internal angles in a simple pentagon total 540°. A pentagram is an example of a self-intersecting pentagon.

Contents

Regular pentagons

A regular pentagon has all sides of equal length and all interior angles are equal measure (108°). It has five lines of reflectional symmetry and it has rotational symmetry of order 5 (through 72°, 144°, 216° and 288°). Its Schläfli symbol is {5}. The chords of a regular pentagon are in golden ratio to its sides.

The area of a regular convex pentagon with side length t is given by

A = \frac{{t^2 \sqrt {25 + 10\sqrt 5 } }}{4} = \frac{5t^2 \tan(54^\circ)}{4} \approx 1.720477401 t^2.

A pentagram or pentangle is a regular star pentagon. Its Schläfli symbol is {5/2}. Its sides form the diagonals of a regular convex pentagon – in this arrangement the sides of the two pentagons are in the golden ratio.

When a regular pentagon is inscribed in a circle with radius R, its edge length t is given by the expression

t = R\ {\sqrt { \frac {5-\sqrt{5}}{2}} } = 2R\sin 36^\circ = 2R\sin\frac{\pi}{5} \approx 1.17557050458 R.

Derivation of the area formula

The area of any regular polygon is:

A = \frac{1}{2}Pa

where P is the perimeter of the polygon, and a is the apothem. One can then substitute the respective values for P and a, which makes the formula:

A = \frac{1}{2} \times \frac{5t}{1} \times \frac{t\tan(54^\circ)}{2}

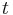with t as the given side length. Then we can then rearrange the formula as:

A = \frac{1}{2} \times \frac{5t^2\tan(54^\circ)}{2}

and then, we combine the two terms to get the final formula, which is:

A = \frac{5t^2\tan(54^\circ)}{4}.

Derivation of the diagonal length formula

The diagonals of a regular pentagon (hereby represented by D) can be calculated based upon the golden ratio φ and the known side T (see discussion of the pentagon in Golden ratio):

\frac {D}{T} = \varphi = \frac {1+ \sqrt {5} }{2} \ ,

Accordingly:

D = T \times \varphi \ .

Chords from the circumscribing circle to the vertices

If a regular pentagon with successive vertices A, B, C, D, E is inscribed in a circle, and if P is any point on that circle between points B and C, then PA + PD = PB + PC + PE.

Construction of a regular pentagon

A variety of methods are known for constructing a regular pentagon. Some are discussed below.

Euclid's methods

A regular pentagon is constructible using a compass and straightedge, either by inscribing one in a given circle or constructing one on a given edge. This process was described by Euclid in his Elements circa 300 BC.[1]

Richmond's method

One method to construct a regular pentagon in a given circle is as follows:[2]

Construction of a regular pentagon

Verification

Richmond pentagon 1.PNG
Richmond Pentagon 2.PNG

The top panel describes the construction used in the animation above to create the side of the inscribed pentagon. The circle defining the pentagon has unit radius. Its center is located at point C and a midpoint M  is marked half way along its radius. This point is joined to the periphery vertically above the center at point D. Angle CMD  is bisected, and the bisector intersects the vertical axis at point Q. A horizontal line through Q intersects the circle at point P, and chord PD is the required side of the inscribed pentagon.

To determine the length of this side, the two right triangles DCM and QCM are depicted below the circle. Using Pythagoras' theorem and the known two sides, the hypotenuse of the larger triangle is found as √5/2. Side h of the smaller triangle then is found using the half-angle formula:

\tan ( \phi/2) = \frac{1-\cos(\phi)}{\sin (\phi)} \ ,

where cosine and sine of ϕ are known from the larger triangle. The result is:

h = \frac{\sqrt 5 - 1}{4} \ .

With this side known, attention turns to the lower diagram to find the side s of the regular pentagon. First, side a of the right-hand triangle is found using Pythagoras' theorem again:

a^2 = 1-h^2 \�; \ a = \frac{1}{2}\sqrt { \frac {5+\sqrt 5}{2}} \ .

Then s is found using Pythagoras' theorem and the left-hand triangle as:

s^2 =b^2+a^2 = (1-h)^2 + a^2=\left(\frac{5-\sqrt 5}{4} \right) ^2 + 1 - \left( \frac{\sqrt 5 -1}{4} \right)^2 \
=\frac {5-\sqrt 5}{2} \ .

The side s is therefore:

s = \sqrt{ \frac {5-\sqrt 5}{2}} \ ,

a well established result.[3] Consequently, this construction of the pentagon is valid.

Alternative method

An alternative method is this:

Constructing a pentagon
  1. Draw a circle in which to inscribe the pentagon and mark the center point O. (This is the green circle in the diagram to the right).
  1. Choose a point A on the circle that will serve as one vertex of the pentagon. Draw a line through O and A.
  2. Construct a line perpendicular to the line OA passing through O. Mark its intersection with one side of the circle as the point B.
  3. Construct the point C as the midpoint of O and B.
  4. Draw a circle centered at C through the point A. Mark its intersection with the line OB (inside the original circle) as the point D.
  5. Draw a circle centered at A through the point D. Mark its intersections with the original (green) circle as the points E and F.
  6. Draw a circle centered at E through the point A. Mark its other intersection with the original circle as the point G.
  7. Draw a circle centered at F through the point A. Mark its other intersection with the original circle as the point H.
  8. Construct the regular pentagon AEGHF.

Carlyle circles

Method using Carlyle circles

The Carlyle circle was invented as a geometric method to find the roots of a quadratic equation.[4] This methodology leads to a procedure for constructing a regular pentagon. The steps are as follows:[5]

  1. Draw a circle in which to inscribe the pentagon and mark the center point O.
  2. Draw a horizontal line through the center of the circle. Mark one intersection with the circle as point B.
  3. Construct a vertical line through the center. Mark one intersection with the circle as point A.
  4. Construct the point M as the midpoint of O and B.
  5. Draw a circle centered at M through the point A. Mark its intersection with the horizontal line (inside the original circle) as the point W and its intersection outside the circle as the point V.
  6. Draw a circle of radius OA and center W. It intersects the original circle at two of the vertices of the pentagon.
  7. Draw a circle of radius OA and center V. It intersects the original circle at two of the vertices of the pentagon.
  8. The fifth vertex is the intersection of the horizontal axis with the original circle.

Direct method

A direct method using degrees follows:

  1. Draw a circle and choose a point to be the pentagon's (e.g. top center)
  2. Choose a point A on the circle that will serve as one vertex of the pentagon. Draw a line through O and A.
  3. Draw a guideline through it and the circle's center
  4. Draw lines @ 54 degrees (from the guideline) intersecting the pentagon's point
  5. Where those intersect the circle, draw lines @ 18 degrees (from parallels to the guideline)
  6. Join where they intersect the circle

After forming a regular convex pentagon, if you join the non-adjacent corners (drawing the diagonals of the pentagon), you obtain a pentagram, with a smaller regular pentagon in the center. Or if you extend the sides until the non-adjacent ones meet, you obtain a larger pentagram. The accuracy of this method depends on the accuracy of the protractor used to measure the angles.

Simple method

A simple method of creating a regular pentagon from just a strip of paper is by tying an overhand knot into the strip and carefully flattening the knot by pulling the ends of the paper strip. Folding one of the ends back over the pentagon will reveal a pentagram when backlit.

Pentagons in nature

Plants

Pentagonal cross-section of okra.

Morning glories, like many other flowers, have a pentagonal shape.

The gynoecium of an apple contains five carpels, arranged in a five-pointed star

Starfruit is another fruit with fivefold symmetry.

Animals

A sea star. Many echinoderms have fivefold radial symmetry.

An illustration of brittle stars, also echinoderms with a pentagonal shape.

Pentagons in tiling

A pentagon cannot appear in any tiling made by regular polygons. To prove a pentagon cannot form a regular tiling, 360 / 108 = 3 1/3, which is not a whole number. More difficult is proving a pentagon cannot be in any tiling made by regular polygons:

There are no combinations of regular polygons with 4 or more meeting at a vertex that contain a pentagon. For combinations with 3, if 3 polygons meet at a vertex and one has an odd number of sides, the other 2 must be congruent. For the pentagon, this results in a polygon whose angles are all (360 − 108) / 2 = 126 degrees. To find the number of sides this polygon has, the result is 360 / (180 − 126) = 6 2/3, which is not a whole number. Therefore, a pentagon cannot appear in any tiling made by regular polygons.

In-line notes and references

  1. ↑ George Edward Martin (1998). Geometric constructions. Springer. p. 6. ISBN 0387982760. http://books.google.com/books?id=ABLtD3IE_RQC&pg=PA6. 
  2. ↑ The animation is based upon a method described by Herbert W Richmond (1893). "Pentagon". http://mathworld.wolfram.com/Pentagon.html.  and further discussed in Peter R. Cromwell (1999). Polyhedra. Cambridge University Press. p. 63. ISBN 0521664055. http://books.google.com/books?id=OJowej1QWpoC&pg=PA63. 
  3. ↑ This result agrees with Herbert Edwin Hawkes, William Arthur Luby, Frank Charles Touton (1920). "Exercise 175". Plane geometry. Ginn & Co.. p. 302. http://books.google.com/books?id=eOdHAAAAIAAJ&pg=PA302. 
  4. ↑ Eric W. Weisstein (2003). CRC concise encyclopedia of mathematics (2nd ed.). CRC Press. p. 329. ISBN 1584883472. http://books.google.com/books?id=Zg1_QZsylysC&pg=PA329. 
  5. ↑ Duane W DeTemple (1991). "Carlyle Circles and the Lemoine Simplicity of Polygon Constructions". The American Mathematical Monthly 98 (2): 97-108. http://apollonius.math.nthu.edu.tw/d1/ne01/jyt/linkjstor/regular/1.pdf.  JSTOR link

See also

External links

Polygons
Listed by number of sides
1–10 sides
Henagon (Monogon) · Digon · Triangle (Trigon) · Quadrilateral (Tetragon) · Pentagon · Hexagon · Heptagon · Octagon · Nonagon (Enneagon) · Decagon
11–20 sides
Hendecagon · Dodecagon · Triskaidecagon · Tetradecagon · Pentadecagon · Hexadecagon · Heptadecagon · Octadecagon · Nonadecagon (Enneadecagon) · Icosagon
Others
Apeirogon
Star polygons
Pentagram · Hexagram · Heptagram · Octagram · Enneagram · Decagram · Hendecagram · Dodecagram